The Pythagorean Theorem
Toward the end of the movie "The Wizard of Oz," the Scarecrow, having just received a brain, makes a mathematical statement to prove how smart he has become:

image from https://9gag.com/gag/amB86Y4
Unfortunately for the Scarecrow, his new brain doesn't seem to have memorized this rule correctly, and he's made several mistakes.
The rule that the Scarecrow is trying to quote is known as the Pythagorean Theorem. It's named after Pythagoras, the Greek mathematician and philosopher who first discovered this principle of mathematics.
What the Pythagorean Theorem actually says is that the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse. You may also know it as a² + b² = c².
So what the heck does that even mean?
First, the Pythagorean Theorem deals specifically with right triangles (not isosceles, as the Scarecrow stated). This means it applies in any triangle that has a perfect 90° angle. You'll see this most often in cases where one side of the triangle is vertical and one side is horizontal, although this doesn't always have to be the case.
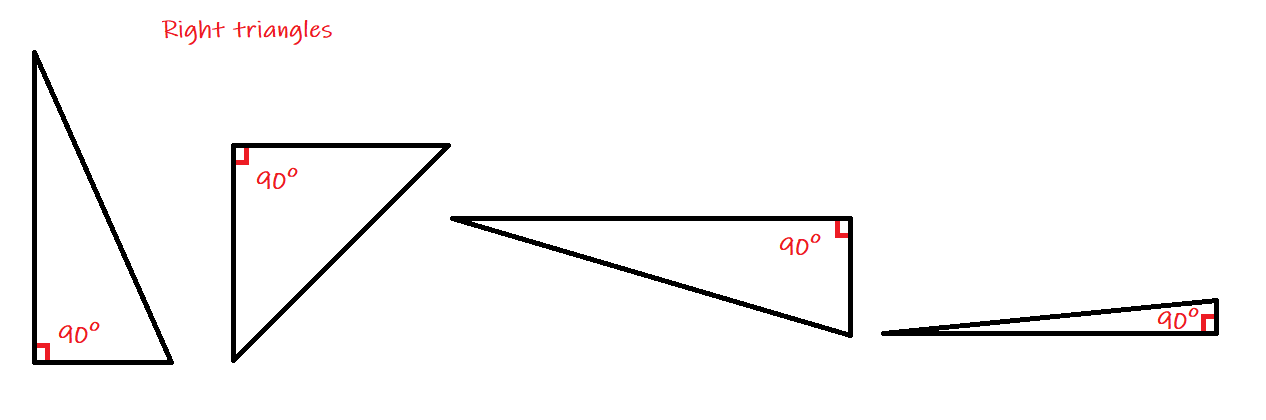
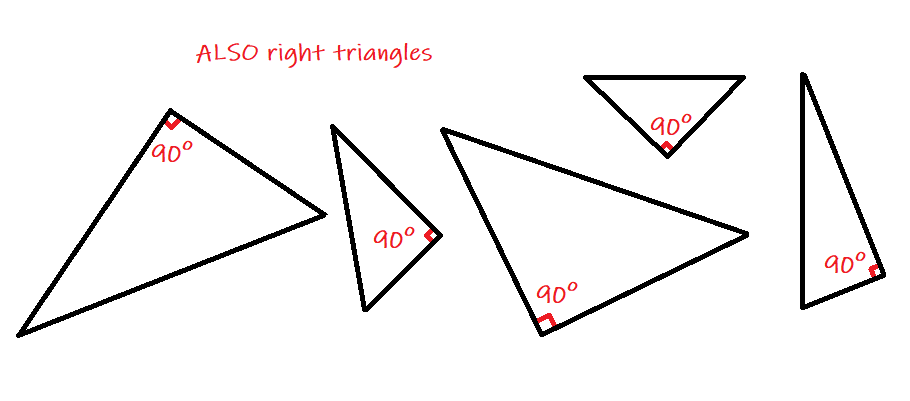
Next, hypotenuse is a fancy word that means the longest side of the triangle. In a right triangle, it's always the one across from the right angle. Meanwhile, the other two sides of the triangle that aren't the hypotenuse are referred to as legs.
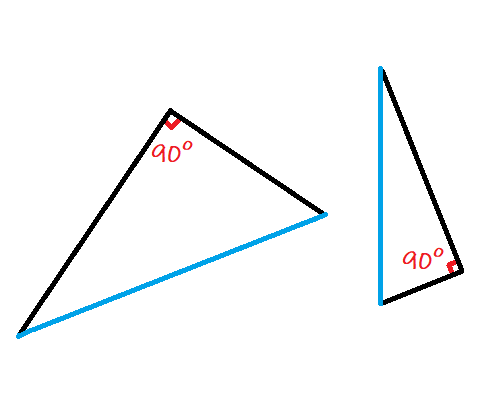
(The hypotenuse of each triangle pictured here is marked in blue.)
So the Pythagorean theorem tells us that if we take the lengths of the two short sides, square them, and add them together, the result will be the square of the length of the long side.
For example, consider this triangle:
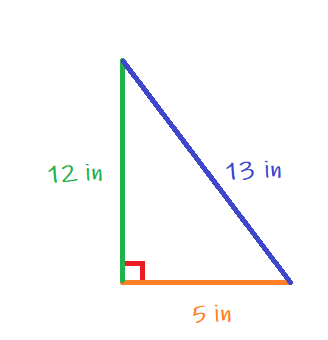
The legs of this triangle have lengths of 12 inches and 5 inches, and the hypotenuse is 13. According to Pythagoras, if we take 12 and 5, square them, and add them together, we should get 13 squared. Let's test that theory:
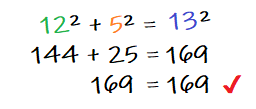
Pythagoras' Theorem tells us that this should work for the side lengths of any right triangle, no matter how big or small. We represent this relationship by calling the leg lengths "a" and "b" and the hypotenuse "c".
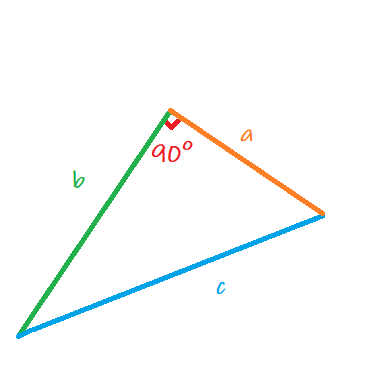
This allows us to write the rule as that classic equation: a²+b²=c². So now you know!
