Common Core Math for non-teachers

As a math teacher in the 2020's, I get asked a lot "do you teach that Common Core Math stuff?" with a tone that suggests that Common Core Math is something you find on the bottom of your shoe. I usually say "yes" and explain why that's not as bad as you may think it is. Most people don't understand what "Common Core" actually is and how it affects what their child is learning in school. 

First off, Common Core isn't actually a type of math at all. The Common Core is a set of core standards - i.e. a list of what students are expected to learn at various levels of their education. For example, standards like "by the end of kindergarten, you should be able to count to 100" or "fifth graders should be able to add together fractions with different denominators." It's called the Common Core because it's intended for these  standards to be shared by all 50 states of the US. That way, if a third-grader moves from  Michigan to California, they won't find themselves behind in math because Michigan waits until fourth grade to teach a topic that California covers in second grade.

Ok, so consistency across states makes sense - so then why is my child learning this weird stuff?

One of the things that is emphasized in the Core Standards is a building of number sense. It's not enough to know what to do with numbers; you should also understand why you're doing those things. So when concepts are initially being taught, they'll often be broken down to include steps that demonstrate the underlying concepts of the algorithm - in other words, before teaching them the "normal way," they get taught the "hard way" so they understand what's going on under the hood.

For example, consider the addition problem 397 + 435.

If you're trying to solve this the "normal way" (the way you remember from your own elementary school days), the process goes something like this: "7 plus 5 is 12, carry the one; 1 plus 9 plus 3 is 13, carry the one; 1 plus 3 plus 4 is 8; so the answer is 832."

On the other hand, if you're trying to solve this off the top of your head with no calculator and no paper, you might do something like this: "well, 397 is three away from 400, so move 3 from the 435 to the 397. Now it's 400 plus 432, so the answer is 832." Much simpler, right? That's not the rule you learned in school; it's your number sense.

Just as you mentally break apart the 435 into multiple pieces to add them together, your child has probably been taught to split up 435 into four 100's, three 10's, and five 1's. So on a homework assignment, they might use a number line to start at 397 and do jumps of those hundreds, tens, and ones until they get to the right answer.

 

Another thing they might do is use number blocks: 397 and 435 each get broken up into sets of 100's, 10's and 1's, which then get combined into groups:

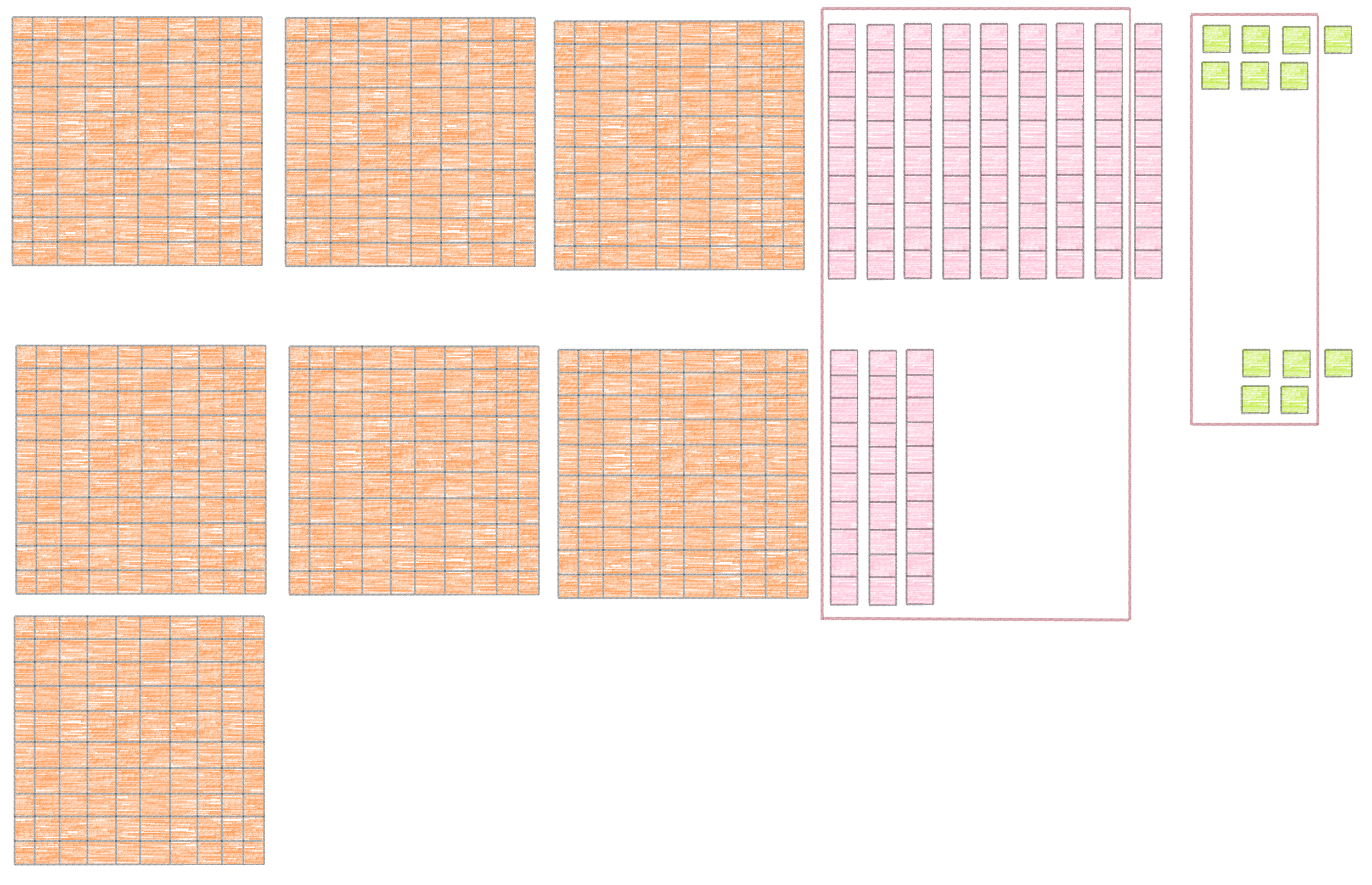
Will they always use the number lines or number blocks to do addition like this? Of course not! But doing it this way first will help them understand how the "normal way" works, which will help them be better at it in the long run. It will help them see WHY they need to "carry the one" so that they're never confused about whether it's the 1 or the 3 that needs to be "carried" from the 13.

One more example: do you remember how to work with fractions? If you're like most of the people I've talked to, you may remember the phrase "common denominator," but you don't remember whether to use it for addition or multiplication, and you don't remember when or how you're supposed to do the "flip it upside-down thing." Chances are, when you learned how to work with fractions, you were taught a set of rules for working with them, but never really understood how or why the rules worked the way they do.

Meanwhile, under the common core standards, elementary school students will use "visual fraction models" to represent various ways of working with fractions. By doing this, they'll gain a more intuitive understanding of why a common denominator is necessary for addition and subtraction, and why dividing fractions involves flipping one of the fractions upside-down. The approaches that seem confusing and long-winded to you as a parent will actually make it easier to understand and remember later.